Bridging computational thinking research and practice of pre-service and in-service teachers

We conducted a systematic review to find out what type of guidance is provided to teachers about computational thinking and what the most common definitions researchers use in the professional training they organize. This review allowed us to select forty articles that were analyzed according to their objectives, theoretical basis, adopted definitions of CT, the scope of CT, and the CT skills addressed. Some studies might appear to meet the inclusion criteria, but were excluded. For example, the study (Zhao et al. 2020) where the treated research question was: “Can Scratch online PD course based on MIT CT framework positively promote the teaching self-efficacy in CT of in-service teachers?”. The paper has as a central theme CT and Scratch environment and does not provide an explicit relationship to STEM subjects.

As a result of step number 3 in the PRISMA process flow: Include, the results of the analysis were presented according to the research questions below. The papers were analyzed according to their objectives, theoretical basis, CT definitions, CT Scope, and CT elements.

We did use some qualitative methods (keyword analysis and Jaccard Index) but they are not statistical syntheses of the results.

Regarding the systematic literature review

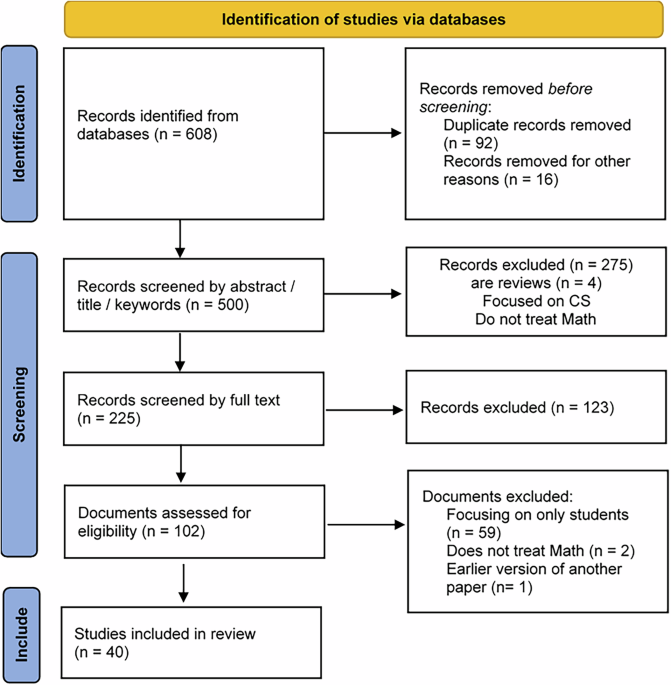
To outline the systematic review process step by step, we followed the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) flowchart as part of the reporting process. Figure 1 illustrates the PRISMA^{Footnote 2} flowchart as a result of our systematic review. It encompassed all data recomplicated from the designated databases.

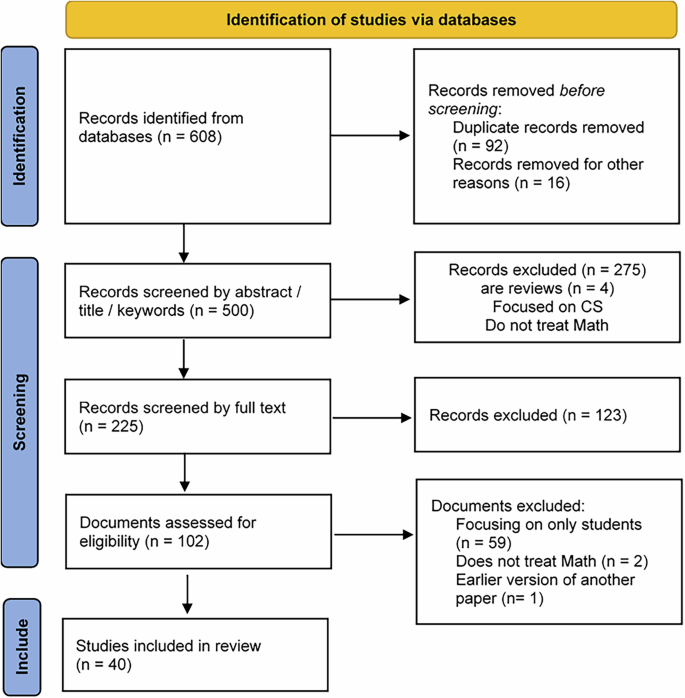
Study selection process flow PRISMA 2020.

We also present an example of SCOPUS in Table 2. The development of the String Search (SS) can be observed. And depending on the search engine and the specificity of each one, we settled for those final search strings shown in Table 2.

As we conducted our review, we identified two distinct categories of articles: experiential (EXP), which focuses on practical experiences and/or courses, and theoretical (TH), which adopts a more theoretical approach. Eight papers (Rambally, 2014, 2015; Rosamond, 2018; Sinkovits and Soto, 2020; Sanford, 2018; Temerbekova et al. 2021; Voskoglou et al. 2020; Weintrop et al. 2016) are either presenting examples, presenting a taxonomy, activities or a tool.

Preliminary scope study

We present statistical data encompassing information and provide valuable insights into the landscape of computational thinking integration in education, focusing on the target populations and the qualifications of educators. Subsequently, we outline the research questions and objectives, the CT skills imparted by the researchers, and the CT skills addressed by educators throughout the academic levels.

Target population and type of trained teachers

Then, we were interested in uncovering the target population. We initially categorized the target population: “Did the article target only teachers, or did it focus on teachers and their students?”. 65,8% of the studies focused only on teachers and the rest on both. The second round was more teacher-focused, as we noted that the studies targeted different types of teachers; most studies (70%) targeted in-service teachers, while 22.5% involved pre-service teachers.

In our systematic review, we investigated possible causes of heterogeneity among the study results to understand the variability and draw more conclusive interpretations. We found out that most lead researchers are from the US since it was popularized by Pr. Wing from the University of Carnegie-Mellon (this is true for 59% of the studies). We had the first categorization, in terms of target population: “Did the paper targeted teachers alone or was it interested in teachers and their students?”. 66% of the papers trained teachers only.

Then the second round of filter was focused on the teachers, since we noted that studies were targeting different types of teachers; Most studies (30%) targeted Pre-Service Teachers (PSTs). Knowing that their academic level, included only Elementary and Middle school PSTs. For this specific population, only one study was interested in working both ways. The rest of the studies focused on integrating CS/CT within the Math or STEM subject. This is the objective behind our future research.

We believe that research should focus more on Pre-Service Teachers since they are the teachers of tomorrow, and by offering a training that helps integrate computer science (CS) and computational thinking (CT) into STEM (Science, Technology, Engineering, and Mathematics) education. This way, we can develop those skills via different materials. We did appreciate the fact that the training was done in a balanced manner between Plugged and Unplugged ways. Although talking in general we see that 42.5% of the PD was conducted the Plugged way, 15% Unplugged, and 35% opted for a mixed approach. We would encourage researchers to start and focus on an Unplugged Professional Development since it is more inclusive and can be carried out in any context.

CT skills taught

Figure 2 illustrates the fact that researchers mainly focused on Abstraction (Identifying the main issue by simplifying its complexity, distilling essential information, and constructing a system representation) (Bouck and Yadav, 2022; Rich et al. 2020) and Algorithmic thinking (Employing a sequential thought process for Problem-Solving) (Jocius et al. 2020; Mardi, 2020). Generalization (Recognize patterns, commonalities, and relationships; analyze new problems by drawing parallels with those already resolved) (Maharani et al. 2021) and decomposition (Consider issues by deconstructing them into smaller, more manageable components) (Bouck et al. 2021; Rich et al. 2020) were also used as CT skills.

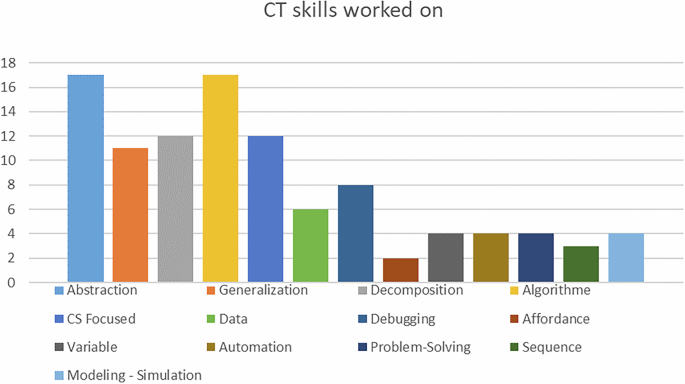
CT skills addressed by academic level

Intending to analyse the relationship between CT skills treated and the academic level targeted, we established Fig. 3.

• In primary school, the study of abstraction, patterns, decomposition, and Algorithmic thinking was studied even. Then, we can see the Data and debugging.

• In middle school, the two dominant skills studied are abstraction and algorithmic thinking.

• In high school, we noted a peak in abstraction, and the studies were very CS-focused.

• At the university level, only a few studies were oriented toward training university teachers, only 5%.

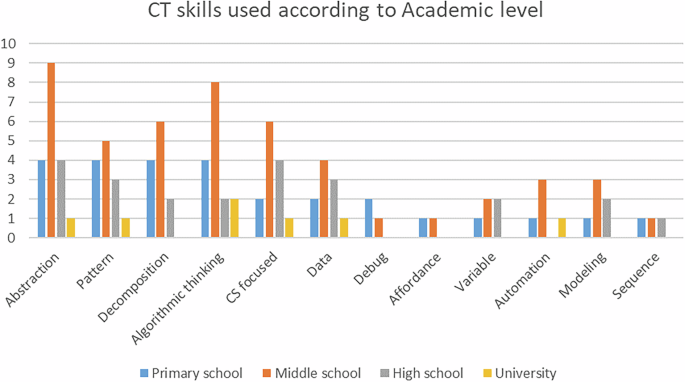
CT skills used according to academic levels.

Objectives of Research Questions addressed

We can see from Table 3, in terms of the addressed objectives and research questions, that the majority (82.5%) aimed to address the integration of CT into the curriculum and help teachers understand and graft it onto the already established curriculum either by proposing a learning trajectory or via case studies.

Lesson plan elaboration (30%) and presentation of examples (20%) were also very popular. It is a way of showing teachers how to integrate CT into their teachings, and teachers appreciate it. Special education could have been better represented, only 5%. One paper worked with preservice teachers in preparation to become special education teachers for students with disabilities or those at risk of disability. The other presented activities for teachers to help them expose and engage students with disabilities in CT and CS. And 10% of the papers offered a methodology.

In other words, for the target population and teacher training, a noteworthy emphasis on in-service teachers (70%) compared to pre-service teachers (22.5%). This focus suggests recognizing the importance of continuous professional development for teachers already in STEM disciplines (Hayward et al. 2016). There should be more focus on pre-service teachers and include it in their training.

Regarding the objectives and addressed CT Skills, most studies (82.5%) are geared towards integrating CT into the curriculum, indicating a clear emphasis on curriculum development and instructional strategies.

Across academic levels

In primary school, a comprehensive set of skills (including abstraction, patterns, decomposition, algorithmic thinking, data, and debugging) is covered. In this sense, it was interesting to note that while abstraction is considered a pilar skill for CT, it was not widely addressed in primary education (Fig. 3); the reason might be related to Piaget’s theory of cognitive development, where he affirms that Abstraction can be developed starting at age 12 (Barrouillet, 2015; Kramer, 2007; Lister, 2011) even though studies are working on this age frame to demonstrate that primary students are capable and should be taught abstraction (Sys\lo and Kwiatkowska, 2014; Waite et al. 2016). As students progress to middle school, the scope narrows to abstraction and algorithmic thinking. However, the limited focus on university-level training (5%) raises questions about the preparedness of higher education institutions to integrate CT into their teacher training programs.

Then we worked on our two Research Questions: “RQ1: What is the relationship between CS-CT & CT-Math?” and RQ2: “What is the definition most researchers transfer to teachers about CT and CS via PD and what is taught?”.

RQ1: What is the relationship between CS-CT & and CT-Math?

To have an idea of when the interest in training STEM teachers to integrate CT into their mathematical classroom (Lockwood and Mørken, 2021), Fig. 4 shows the type of publication by year. It started around 2010 (knowing that Computational Thinking gained prominence in 2006, given the dissemination paper by Professor Wing), and we noted a peak in 2020. We can see that conference papers are the leading publication mean used. It is followed by journal articles and, finally, chapter books.

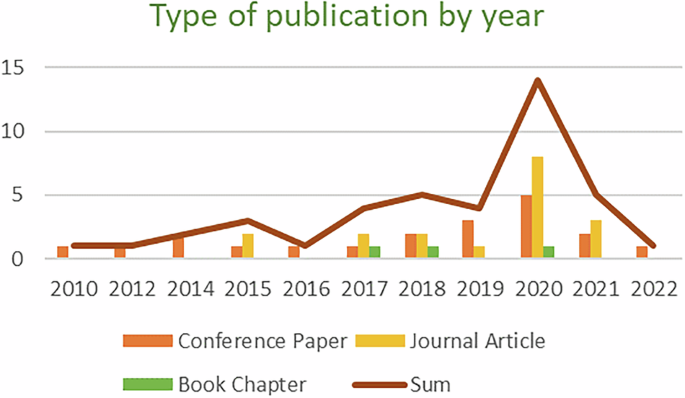
Type of publication by year.

Looking closer at the way professional development was conducted, we found out that:

• 42.5% of the PD was conducted the Plugged way, using activities involving computers, digital devices, or technology in general. Engage with software, coding platforms, or online resources. Excel, Sphero (Programmable Robots), BBC micro: bit, and digital tangibles were used as tools.

• 15% Unplugged, using activities that do not rely on computers or digital technology. They could involve physical exercises, games, puzzles, and interactive group activities without the need for digital devices. The papers’ authors used Rubrics, Lesson plans, Field Trips, and CS Unplugged activities.

• 35% adopted a mixed approach.

Analysing the papers, 45% of the papers treated CS alongside CT, and the rest were equally divided between papers focused on CS and other documents focused on CT. To delve deeper into this relationship, we investigated, as illustrated in Fig. 5, to discern the researchers’ focus. Specifically, we examined the extent to which their objective involved the integration of CT into the STEM domain. Only 5% of the reviewed papers exhibited such an integration.

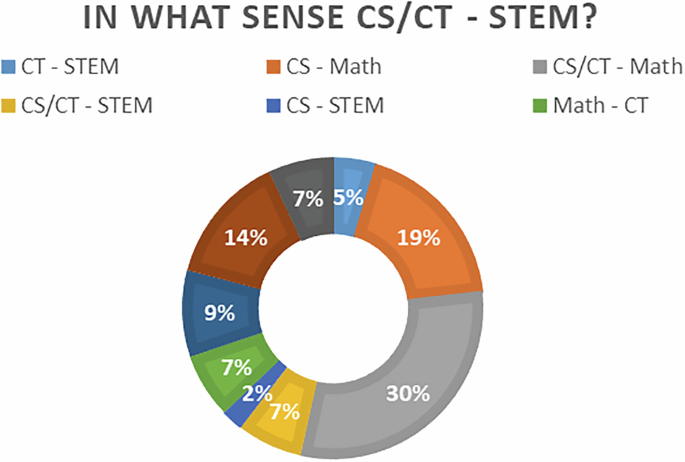
In what sense is CS/CT-STEM taught?

Looking more closely at how professional development was conducted, we wanted to uncover the supposed relationship between Computer Science and Computational Thinking. When opting for a connected mode of teaching CT, authors used various tools; some are specific to CT (scratch, Sphero), and others are technological tools (Excel, programmable robots) used to enhance CT skills. A third of the studies used both approaches. Most of the studies (42.5%) preferred a connected approach.

In this sense, nearly half of the papers treated CS alongside CT. This supports the idea that CT’s origin is closely related to computer science (Li, 2014). However, since it is defined as a thought process, more researchers are studying the transferability of Computational thinking skills and expanding it to more areas and subjects. Knowledge Transfer (KT) involves effectively applying knowledge, skills, and attitudes gained from education or training programs. KT serves as a basis for future learning. KT plays a crucial role in making information portable, enabling students to apply it in new environments creatively and innovatively. This transfer occurs using meanings, expectations, generalizations, concepts, or perceptions developed in previous situations and applied to future ones (Gutiérrez-Núñez et al. 2022). For example, in their systematic review (J. Ye et al. 2022), the authors examined 55 empirical studies and analyzed the transfer of CT using a meta-analysis and a qualitative synthesis. They identified the effects of CT, beyond CS, in the fields of mathematics, science, engineering, and the humanities. 39 of 55 studies focused on mathematics and natural science due to the close relationships between CT, mathematics, and science. There is a growing interest in integrating CT in non-STEM fields (language learning, social science, and music).

The findings of the meta-analysis demonstrated an overall positive and significant impact in transferring Computational Thinking skills to other academic disciplines. Furthermore, the statistical analysis provided confirmation that CT skills can be successfully applied and transferred to various subject areas, encompassing both STEM and non-STEM fields. This finding supports the idea of both near and far transfers of CT skills. Additionally, authors judged it as being positive for students’ learning.

Discussion of the RQ1

Our systematic review focuses on collecting and analyzing PD experiments that teach about CT and, more specifically, infusing CT into STEM in general and Mathematics in particular (H. Ye et al. 2023). So, it was interesting to note that more and more authors are interested in this approach. The interest in training STEM teachers to integrate CT into their mathematical classrooms started in 2010 and is still ongoing. Most of the work is published as journal articles and conference papers. On a deeper level, we noted that the main objective of those studies was to infuse CS/CT into Math classrooms (30%), and some studies did it the other way around: they went from Mathematics to introduce Computational Thinking.

In this optic of infusion, the K-12 CS framework (Framework, 2016) represents the relationship between computer science, science and engineering, and math practices. Since we are not working on science or engineering, we will only consider the relationship displayed between CS and Math. As it is presented, they both develop and use abstractions (reason abstractly and quantitatively, developing and using abstractions), use tools when collaborating (use appropriate tools strategically and collaborating around computing), and communicate precisely (attend to precision and communicating about computing).

Looking at the same relationship obtained from the analysis of the papers of the Systematic Review, we got this relationship the following: “abstraction, communicating, conceptual knowledge, developing, iteration, logical thinking, modeling, and simulation” as standard features between CS and Math. Also, the use and development of abstraction overlap for the three components we are considering (CT, CS, and Math). Also, communication and collaboration are at the heart of CS and CT.

Considering Shute’s paper (Shute et al. 2017) and their two circles, the Venn Diagram shows the similarities and differences between CT and mathematical thinking. When we focus on the overlap between Computational thinking and Math, Shute et al. offer Problem-Solving, modeling, Data analysis and interpretation, and Statistics and probability. Comparing it with the results from the Literature Review, we note that Statistics is reserved for Math’s definition. Modeling and problem reduction are joint between CT and Math. But again, problem-solving and Data analysis are standard components for the 3 (CS-CT-Math).

Looking at individual definitions, most of the notions in MT are included in what we call BoK (algebra, calculus, geometry, etc.). We also have programming as a standard between CS and CT. Programming results from developing CT skills, as cited by Israel et al. 2015 and mentioned by Shute et al. 2017. We agree with Shute’s conclusion that CT is an umbrella term.

The central shared concept of CT and MT is Problem-Solving (Wing, 2008). This is one of the reasons why we focused more on problem-solving in future work.

We also adopted a manual analysis of the different definitions from our systematic examination, allowing us to identify the concepts or technologies employed by researchers to define CT, CS, or Mathematics. However, we noted that researchers need to be in the habit of defining Mathematics. Manually, we uncovered 31 words to define CT, 21 for CS, and 19 for Mathematics. However, the research with the script revealed 35 words to define CT, 17 for CS, and 17 for Mathematics. Merging the two approaches, we found similarities and other concepts proper to each area (see Fig. 6).

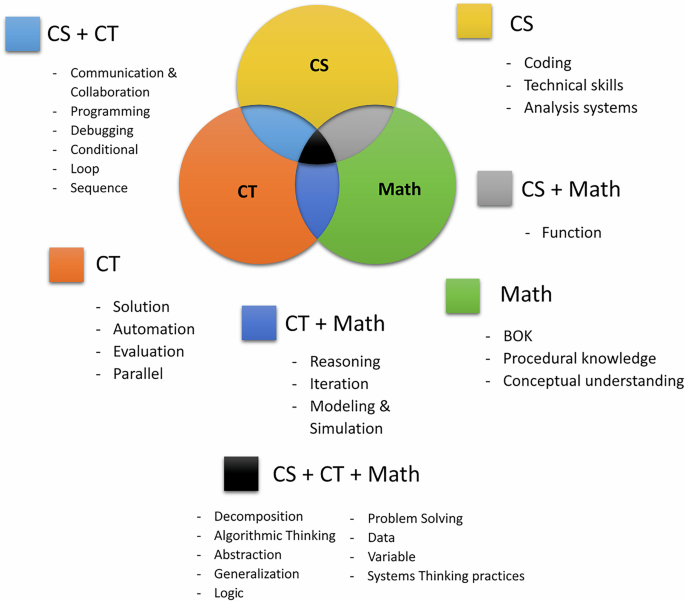
Relationships between computer science, Computational thinking, and math from analysing the definitions the researchers used in the researched articles.

Some terms were only cited in one article, while other elements appeared in multiple articles. Some elements were integrated with others since they fall under the exact definition or area. It is worth mentioning that the terms used include concepts, skills, and technologies. It was rare for the authors to pinpoint the exact definition they followed (for example, (Weintrop et al. 2016) did it). So, the solution was to rely on the definitions they cited, and then we selected the keywords. Since we had a few values on the extreme ends of our dataset, we used the interquartile range (IQR) to find outliers. Identifying outliers aims to evaluate their influence on the analysis and make well-informed choices regarding their treatment, such as eliminating them or applying suitable transformations.

The Q1 represents the central value of the first half of your dataset, excluding the median. Similarly, the Q3 represents the central value of the second half of your dataset, excluding the median. The IQR, or interquartile range, measures the spread of the middle 50% of your dataset, calculated as the difference between Q3 and Q1. IQR = Q3 – Q1. Then, the upper fence designates the threshold encompassing the third quartile, indicating that any values surpassing this boundary are considered outliers. Conversely, the lower fence denotes the limit surrounding the first quartile, flagging any values falling below this threshold as outliers. The upper and lower fences are calculated respectively as Q3 + (1.5 * IQR) and Q1 – (1.5 * IQR).

For CT, the median is the 16th value. The median value is 3. The first quartile value is Q1 = 10. The third quartile value is Q3 = 3. We obtain IQR = 8. The upper fence is 15, and the lower is 2. For CS, the median is the 11th value. The median value is 2. The first quartile value is Q1 = 5. The third quartile value is Q3 = 2. We obtain IQR = 3. The upper fence is 6.5, and the lower is 0.5. For Math, the median is the 10th value. The median value is 3. The first quartile value is Q1 = 4. The third quartile value is Q3 = 1. We obtain IQR = 3. The upper fence is 5.5, and the lower is 0.5.

So, according to calculation, for CT, our outliers are the ones greater than 15, which means the last four values, and less than 2, which means the first seven values. Our outliers are above 6.5 for CS, which means the previous three values. For Math, our outliers are above 5.5, which means the last three values. So, we have 11 outliers for CT, 3 for CS, and 3 for Math.

Before making a decision (whether we retain the outliers or remove them from our dataset), it is important to consider whether a value is accurate or an error. CT has two sets of outliers: Decomposition, algorithmic thinking, Problem-Solving, and Abstraction. We cannot eliminate those since we believe they are part of the definition we adopted. The second set is Programming, Variable, surprise (CT – Affordance), Loop, Sequence, performance, and Reliability analyses. Those are terms some researchers chose to define CT. Considering that CT’s definition is still a source of discussion, we retain them. The same goes for CS (Algorithms, Logic, Technical Skills). And since we did not encounter legitimate reasons to eliminate Math’s outliers (M&S: Modeling and Simulation, Problem-Solving, BOK (Body of Knowledge)), we retained them. This study’s calculated outliers align with the attributes researchers typically used to define CT, CS, and Math (Osborne and Overbay, 2004). Consequently, [7] elements were identified and subsequently incorporated into our initial definition of CT: Decomposition = [24], Algorithmic thinking = [25], Abstraction = [36], [Solution] = [8], [Evaluation] = [5], [Pattern (Generalization)] = [11], [Problem-Solving] = [27]. And those are included in the definition we adopted.

Accordingly, we obtained the following Venn Diagram. It illustrates the relationship between CS, CT, and math due to the analysis of the definitions the researchers used in the analysed articles.

Here, we present some concepts that were grouped. For example, the BoK in Math covers algebra, geometry, counting, sets, and integers. Problem-solving includes Making sense of problems, problem reduction, creating representations for issues, and problem-solving skills. Communication & Collaboration regroups: fostering an inclusive culture, collaborating, and communicating. Pattern covers matching patterns, patterns, generalization, pattern recognition, and pattern generalization.

In our work, talking about Computational Thinking, we adopted the definition stating that CT is: “Computational Thinking is the thought processes involved in formulating problems and their solutions so that the solutions are represented in a form that can be effectively carried out by an information-processing agent.” (Wing, 2010). It embraces the ability to think algorithmically about decomposition and evaluation, generalizations and abstractions, identifying and using patterns, and choosing good representations.

RQ2: What definition do most researchers transfer to teachers about CT and CS via PD?

To respond to this Research Question, we used three different methods. The methods used were carefully chosen for their completeness since the first method uses word clouds to represent visually the most used words to define computational thinking, computer science, and math based on keyword analysis. Especially in educational research, this method has proven very effective as an exploratory tool when dealing with large text corpora. And if we have a non-specialist audience, it is useful to communicate the results. The second method uses the Jaccard index to analyze the keyword similarity and diversity metrics between the studied concepts. And will help quantify and highlight the overlap between them that may not be immediately apparent. Finally, the third method used ChatGPT, where we gave it the keywords defining each of our concepts (CT, CS, and Math) as input and asked it to guess the concepts relying on the keywords extracted from the reviewed papers.

Using the Word Cloud

Keywords were extracted manually. Considering CT definitions, here is an example of our approach:

• Computational thinking involves “solving problems, designing systems, and understanding human behavior by drawing on the concepts fundamental to computer science.

• Wing (2006) proposes the following working definition of computational thinking: “The thought processes involved in formulating problems and their solutions so that the solutions are represented in a form that can be effectively carried out by an information processing agent: human, computer, or a combination.”

• Computational thinking includes epistemic and representational practices such as problem reduction, transformation, and modularization; recursion and iteration; parallel processing; constructing multiple layers of abstraction; problem decomposition; modeling and simulation; creating representations for problems; and heuristic reasoning.

Notably, the result is bound to bias and interpretation since it was extracted from discursive texts with persuasive goals rather than a systematic representation of the concept. Addressing that, each concept is shown in bold inside an adaptation of a text from the source publication.

We used keywords that defined computational thinking, computer science, and mathematics to form our “white list.” The latter have been used to run our script for each concept. For example, out of all the keywords of the white list to describe CT, the script was able to extract the following:

{‘abstraction’: 56, ‘modeling’: 20, ‘developing’: 15, ‘simulation’: 15, ‘debugging’: 14, ‘logic’: 13, ‘communicating’: 9, ‘iteration’: 8, ‘generalization’: 6, ‘recursion’: 5, ‘collaborating’: 4, ‘parallel processing’: 4, ‘modularization’: 3, ‘modeling’: 3, ‘remixing’: 3, ‘problem reduction’: 3, ‘logical thinking’: 3, ‘abstracting’: 2, ‘data representation’: 2, ‘logical structure’: 2, ‘design process’: 2, ‘pattern generalization’: 2, ‘software engineering’: 2, ‘experimenting’: 1, ‘iterating’: 1, ‘reusing’: 1, ‘modularizing’: 1, ‘constant’: 1, ‘encapsulation’: 1, ‘recursive thinking’: 1, ‘parallel thinking’: 1, ‘iterative logic’: 1, ‘sequential logic’: 1, ‘resource management’: 1, ‘web development’: 1, ‘conceptual knowledge’: 1, ‘data collection’: 1, ‘data analysis’: 1, ‘parallel code’: 1}

The result is shown as a Word Cloud in Fig. 7. Each Word Cloud represents a definition of one of the concepts we are working on (CS, CT, Mathematics). They are based only on the keywords extracted from the definitions provided by the reviewed researchers and may not include some core concepts of CT, CS, or Math. Many researchers may have different insights about these concepts. The “ Discussion “ section will develop the overlap between the three.

a The concept of Computational Thinking. b The concept of Computer Science. c The concept of Math.

The most used words in the selected papers are: “Simulation” and “Modeling,” mainly used to describe Mathematics, “Abstraction” and “Pattern,” attributed to Computational Thinking, and lastly, “Programming,” mainly employed to characterize CS. As illustrated in Fig. 7. This method ensures reproducibility since it is important for the reliability of qualitative analysis methods.

There are different ways of analysing those keywords, inter alia, Keyword Overlap, Frequency, Similarity Metrics, Ranking, and Distribution. We already covered the keyword frequency (Fig. 7).

Analyzing the frequency of the keywords, we can draw some conclusions: The CT concept has a more significant number of keywords (35) (compared to CS and Math). This indicates that the Computational Thinking concept encompasses a broader range of keywords, suggesting diversity and might be related to simulation modeling or software modeling (given the relatively high frequency of ‘modeling’ and ‘simulation’ keywords). The CS concept, since highly identified with ‘web development,’ ‘software engineering,’ and ‘resource management,’ suggests a narrower view of CS related to software development and management. Despite the biases of a few keywords, the math concept is more focused on ‘abstraction,’ ‘logic,’ and ‘developing.’ It seems to be a subset of CS. But in reality, we know that each one of CS and Math has its own Body of Knowledge (BoK).

Using the Jaccard Index

This method is a well-established mathematical tool since it has been widely used and validated. And its reliability is grounded in the fact that it has a clear and replicable formula. Thus, we avoid subjectivity. As is the case for the Word cloud method, the Jaccard index has also been widely used and validated in various fields. Analyzing the keyword similarity metrics between the three concepts, we found: ‘abstraction,’ ‘logic,’ and ‘developing.’ These keywords are fundamental and central to all three concepts. Taking into consideration that the common keywords are 3. The size of the intersection of the two sets is 3. We calculate the Jaccard index between the two different sets:

• CT (35 Keywords) and CS (17 Keywords): ≈ 0.08696 (or approximately 8.70%).

• CT (35 Keywords) and Math (17 Keywords) ≈ 0.08696 (or approximately 8.70%).

• CS (17 Keywords) and Math (17 Keywords) ≈ 0.15789 (or approximately 15.79%).

We can see that the percentage of overlap is relatively low between each pair of concepts, indicating that keyword sets are not very similar except between Math and CS, which is evident since CS is based on Mathematics. The Math concept seems to be a subset or narrower focus of CS. The CT concept emphasizes algorithmic Problem-Solving and iterative process development, and the keywords apply to the broader field of computer science and software development. It should be noted that ’developing’ includes developing a solution with/or without the assistance of an information-processing agent.

Using the ChatGPT

Knowing that our concepts are Concept 1: CT, Concept 2: CS, and the 3 is Math. We asked^{Footnote 3} ChatGPT, relying on the given keywords, to identify the three concepts (without mentioning what each group of words refers to). The result is as follows:

Concept 1: Software Development/Programming Concepts. Key terms with high frequency: abstraction, modeling, developing, simulation, debugging, logic, communicating.

Characteristics: This concept is centered around abstraction, modeling, and the software development process. It involves creating models, debugging code, and utilizing logic to develop and simulate software. Communication is also emphasized in the context of software development.

Concept 2: Computer Science/Programming Fundamentals. Key terms with high frequency: abstraction, logic, developing, debugging, communicating, logical thinking, software engineering.

Characteristics: This concept focuses on the fundamental aspects of logic, abstraction, and the broader field of software engineering. It includes logical thinking, debugging, and effective communication in software engineering.

Concept 3: Computational Modeling/Problem-Solving Key terms with high frequency: modeling, abstraction, simulation, developing, iteration.

Characteristics: This concept revolves around modeling, abstraction, and problem-solving. It emphasizes developing models, simulations, and iterative processes to solve problems. It also includes recursion and modularization as part of the problem-solving approach.

Discussion of the RQ2

Keywords defining our three studied concepts—CT (Computational Thinking), CS (Computer Science), and Mathematics—were manually extracted from the selected articles. We then processed this list through our script, obtaining keywords for each concept, which were visualized using a Word Cloud. The most frequently used words were: “Simulation” and “Modeling” for Mathematics, “Abstraction” and “Pattern” for Computational Thinking, and “Programming” for Computer Science.

We focused on keyword frequency to draw initial conclusions, calculating the Jaccard index to measure similarity. Despite potential biases, this approach provides a reproducible method for qualitative analysis, ensuring the reliability of our findings. The results indicate that CT is richly represented with a broader range of keywords compared to the other two concepts, suggesting it is the most defined concept. CS keywords point to a focus on software development, such as “Web development” and “Software engineering.” Mathematics keywords emphasize “Abstraction” and “Developing,” indicating it as a subset of CS concepts. These keywords provide a more restrictive definition for CS and Mathematics.

By analyzing the keyword similarity metrics between the three studied concepts, we identified ‘abstraction,’ ‘logic,’ and ‘developing’ as common keywords. The results show a relatively low percentage of overlap between each pair, except for CS and Math (approximately 16%). This suggests that CT has distinct keywords broadly applicable to computer science, while Math is a subset of CS.

To analyse the definition of Computational Thinking, we choose the K-12 framework as a reference since it is the result of the collaborative work between the Association for Computing Machinery ( Code.org, Computer Science Teachers Association ( Cyber Innovation Center ( and National Math and Science Initiative ( with states and the computer science education community.

They offer conceptual guidelines for computer science education. The K12 CS framework presents the core practices, including computational thinking. And identify CT as the heart of CS.

They define the core practices as being:

1. (1)

   Fostering an inclusive computing culture.

2. (2)

   Collaborating around computing.

3. (3)

   Recognizing and defining computational problems.

4. (4)

   Developing and using abstractions.

5. (5)

   Creating computational artifacts.

6. (6)

   Testing and refining computational artifacts.

7. (7)

   Communicating about Computing.

CS is delineated by practices 3–6 to decide between CS and CT. The three remaining are independent, general practices in computer science that complement computational thinking. The statement “Computational thinking is essentially a Problem-Solving process that involves designing solutions that capitalize on the power of computers; this process begins before a single line of code is written.” (Framework, 2016) aligns with what we pretend with our research goals. It stresses the fact that Computational Thinking is a human ability (Wing, 2008).

Knowing that Papert and Wing are the two pioneers of Computational Thinking, we examined whether they were referenced in the selected papers. Table 4 shows the papers citing either, both, or neither author.

Additionally, Shute’s paper (Shute et al. 2017) discusses a working definition based on a literature review in K-16 settings. It offers the different definitions of CT, interventions, assessments, and models across various disciplines. Defining CT as: “The conceptual foundation required to solve problems effectively and efficiently (i.e., algorithmically, with or without the assistance of computers) with solutions that are reusable in different contexts.”. It includes six facets of CT: abstraction, decomposition, algorithm design, debugging, generalization, and iteration. Table 5 presents the definitions of CT practices we adopted.

As for the use of ChatGPT, it was a different approach whose objective was to do a reverse engineering process on the collected keywords. Used to further differentiate and identify their characteristics. The keywords were grouped without revealing the specific concept they pertained to and given to the generative IA.

• The first concept, while not optimally named, was accurately described: and identified as centered on practical software development and problem-solving through abstraction, modeling, and effective communication.

• The second is focused on foundational principles and broader aspects of software engineering, logical thinking, and abstraction.

• Again, the last one was provided as a subset of CS emphasizing computational modeling, iterative problem-solving, and creating simulations and models.

This responds to our research question: The first and third concepts were partially accurate, but the second one was accurate. Which is perfectly comprehensible for math since each paper focused on a particular part of it and was not treated as a whole. Also, the traditional view of Mathematics subsuming Computer Science against considering Math as part of the more general discipline of Computing Sciences remains controversial (Rosenbloom, 2012, p. 237) and would require more profound research. As for the first one, it proves once again the difference in definition that exists for CT and also that there is not yet a consensus when defining it (a fact supported by the literature).

Critical analysis across all research questions

Research questions RQ1 and RQ2 are intrinsically linked. Addressing them together allows us to understand not only the interconnection between the disciplines under analysis, but also how this knowledge is defined and imparted to educators. RQ1 explores the relationship between computer science (CS), computational thinking (CT), and Mathematics. The findings of the manuscript indicate a strong connection among these areas, highlighting that nearly half of the studies analyzed address CS together with CT. This finding underscores the origin of CT in CS, but also the growing expansion of CT to other areas and subjects. The manuscript reveals that abstraction is a crucial component shared by the three disciplines, while communication and collaboration are essential for both CS and CT.

The analysis of individual definitions identifies problem-solving as a central concept that unites CT and mathematics. This discovery reinforces the notion that computational thinking is essentially a problem-solving process. Importantly, the K-12 CS framework, a product of collaboration among prominent computer science education organizations, places CT at the core of CS. This framework defines the fundamental practices of CT, including the development and use of abstractions, the creation of computational artifacts, and communication about computing.

The use of the Jaccard Index in the study quantifies the similarity between the sets of keywords defining each concept. The results show that although the overall overlap is low, the similarity between CS and Mathematics is more pronounced than between CT and either of the other two disciplines. This pattern supports the idea that CS is based on Mathematics, but also suggests that CT has a broader scope and can be applied to various areas, including Mathematics.

The study also examines how researchers convey their definitions of CT, CS, and Mathematics to teachers through PD. A surprising finding is that 25% of the reviewed articles make no reference to Papert or Wing, pioneers of CT. This omission raises questions about the depth and accuracy with which fundamental CT knowledge is being transmitted to educators. The study uses the WordCloud method and the Jaccard Index to analyze the definitions of CT, CS, and Mathematics. The results of the WordCloud analysis indicate that CT is represented with a broader range of keywords compared to the other two disciplines. This suggests that CT is the most broadly defined concept, while the CS keywords focus on software development and those of Mathematics on abstraction and development, which could be interpreted as a more limited definition. The analysis of the Jaccard Index reveals a low overlap among the sets of keywords for each pair of concepts, except for CS and Mathematics. This result reinforces the close relationship between CS and Mathematics but also underscores the distinctive nature of CT and its applicability to a variety of fields.